一些观察
首先考虑 tarjan 缩点,如果存在一二类点当且仅当这个 DAG 只有一个入度为 的点且一二类点必定在其中。(假设这个块是 )
如果不存在一类点, 里面的点就全是二类点。
横叉边、前向边很烦,但是如果确定一个一类点之后以它为根就只有树边和返祖边了。
所以大致做法可以分成两部分,找出一个一类点和确定剩下的一二类点。
注意到只要存在一类点, 以外的点和边都可以不考虑(如果 判断一个点是否是一类点的代价能接受)。
讨论范围缩小到 ,因为是一个强连通分量,所以任选一个点作为根所有点都可以走到它。
C 性质
其实就是帮你找到了一个一类点作为根。
任意一个点 ,如果子树内存在 条指向 祖先的返祖边, 一定不是一类点,否则 是否为一类点取决于指向的唯一祖先是否为一类点。
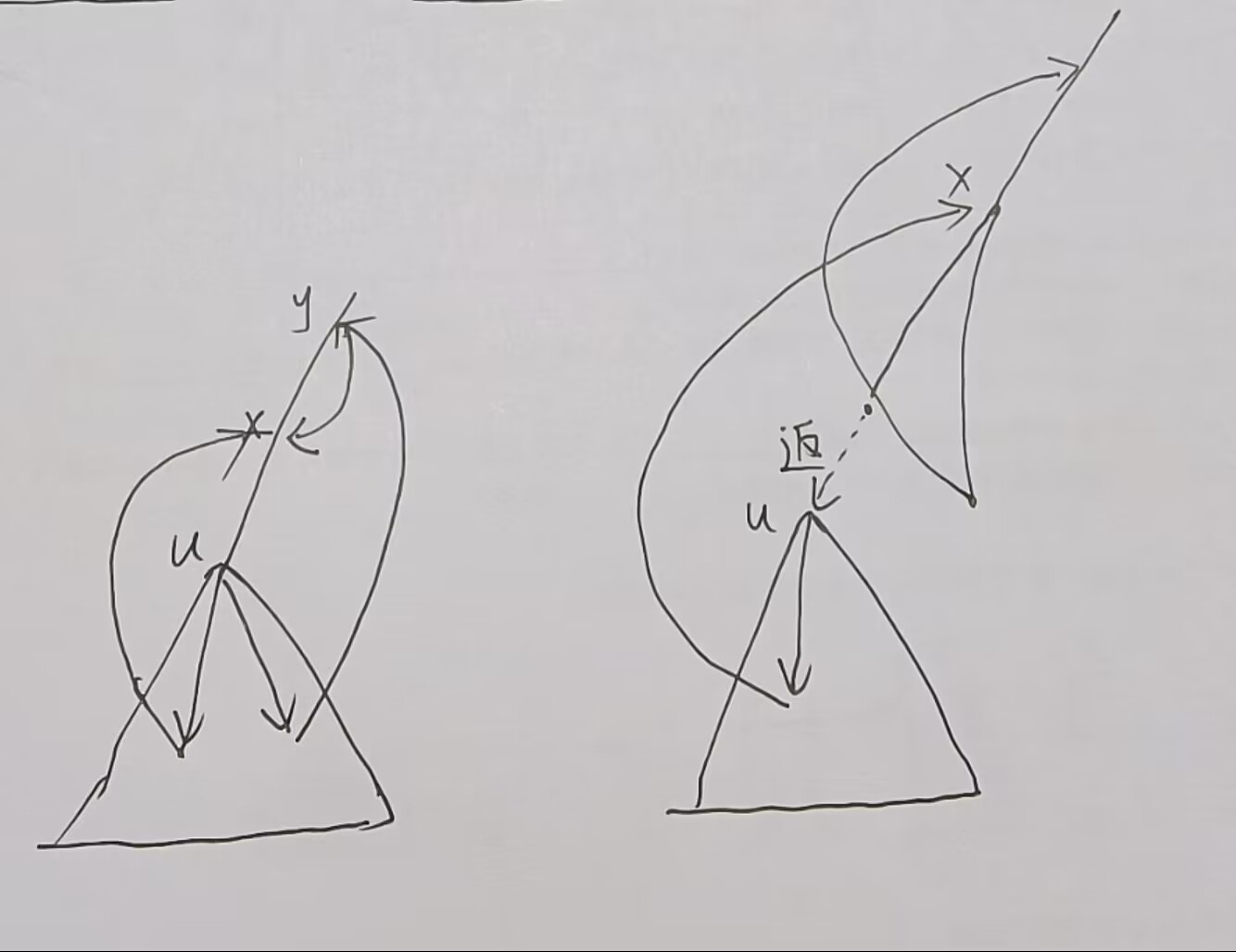
从上往下递推可以找出所有一类点并且标记这些返祖边一定不能删除(下文称为钦定边)。
找二类点我的做法有点像 DP,感觉直接讲实现会清楚一些。
设 表示 是否可能为一二类点,初始 ,然后把所有能够删除的返祖边 存在 这个位置的 vector 里面。
从上往下推:
- 如果 被 条钦定边覆盖,。
- 如果 被 条钦定边覆盖, 取决于唯一出边的那个点。
- 如果没有被钦定边覆盖,当前子树内还有存活的返祖边 ,否则 。
如果 ,删除 vector 里面的所有返祖边。
最后 的点可能成为二类点。
需要写个 BIT 动态维护。
找一个一类点有 。
如何找到一个一类点
随便找一个根,先忽略所有前向边。
任意一个点 ,只有子树内恰好存在 条指向 祖先的返祖边,或者恰好存在 条指向外部的横叉边,且指向的点是一类点才可能是一类点。
画图比较类似,因为是强连通分量,发现有 条到根的路径就矛盾了。
这个依赖关系是一个树,从根开始找肯定死路一条。
对于一个前向边 ,它最后一定是一个返祖边。
对于一个横叉边 ,它最后要么是树边,要么是返祖边。
所以一类点在树上一定在 的子树内。
树边和返祖边最后是互相转化(?)这里我场上猜的,画了好几个图感觉没影响啊。
(就这里如果我当时会证了就不会后半场 T2 了)
找到树上深度最大的 ,在它子树内搜索。
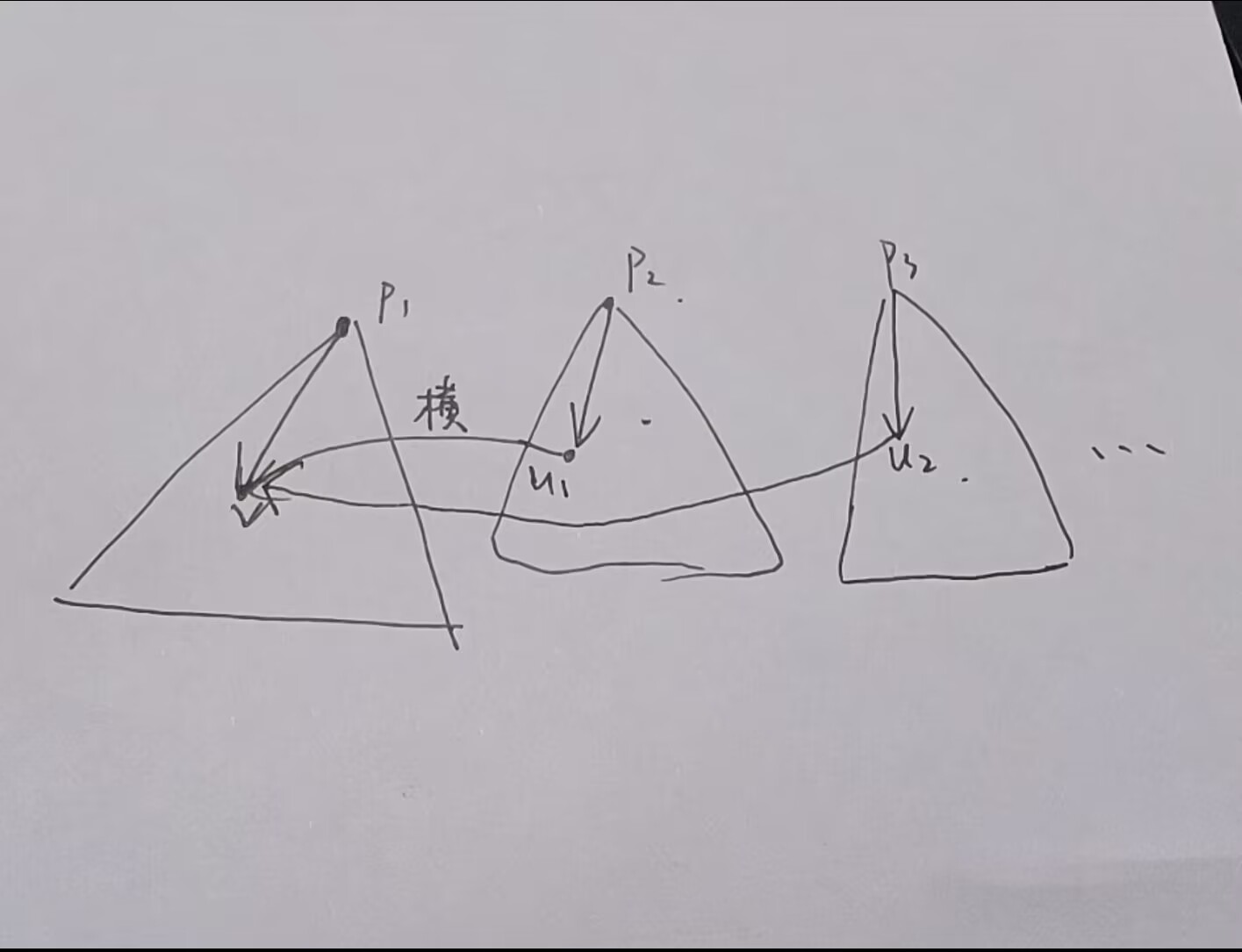
注意到 子树最后一定是形如这样的若干条链(因为子树内不可能有横叉边再进行分叉),所以可能的点就是 和 ,暴力 check 就行了。
时间复杂度 。